Математика оперирует не содержанием вещей, а их структурой, абстрагируя ее из всего того, что дано как целое. Отвлечение от качеств и свойств предмета позволяет выявить у данного предмета его основу, неотъемлемую часть, то, что поставит его в один ряд с непохожими на него, на первый взгляд, предметами. Теория графов – это раздел математики, поэтому и в ней используется принцип отвлечения: не важно, что представляет собой предмет, важно лишь то, является ли он графом, т. е. обладает ли обязательными для графов свойствами.

Прежде чем перейти к изучению способов представления графа, рассмотрим примеры, дадим определение графу и ознакомимся с основными понятиями теории графов. Здесь не будут рассмотрены все аспекты теории графов (этого и не требуется), но, по большой части, те, что понадобятся нам в дальнейшем.

В своей жизни мы, так или иначе, соприкасались с объектами, имеющими структуру графа. К таким объектам относятся разного рода маршруты общественного транспорта: система метрополитена, автобусные маршруту и т.п. В частности, программисту знакома компьютерная сеть, также являющаяся графом (рис. 3.1). Общее здесь это наличие точек, соединенных линиями. Так в компьютерной сети точками являются отдельные серверы, а линиями – различные виды электрических сигналов. В метрополитене первое – станции, второе – туннели, проложенные между ними. В теории графов точки именуется вершинами, или узлами , а линии – ребрами, или дугами . Таким образом, граф – это совокупность вершин, соединённых ребрами.

Вернемся к компьютерной сети. Она обладает определенной топологией, и может быть условно изображена в виде некоторого числа компьютеров и путей их соединяющих. На рисунке ниже в качестве примера показана полносвязная топология .

Рисунок 3.1 – Компьютерная сеть

Это, по сути, граф. Пять компьютеров являются вершинами, а соединения (пути передачи сигналов) между ними – ребрами. Заменив компьютеры вершинами, мы получим математический объект – граф, который имеет 10 ребер и 5 вершин. Пронумеровать вершины можно произвольным образом, а не обязательно так, как это сделано на рисунке.

Вот некоторые важные обозначения, используемые в теории графов:

· G =(V , E ), здесь G – граф, V – его вершины, а E – ребра;

· |V | – порядок (число вершин);

· |E | – размер графа (число рёбер).

В нашем случае (рис. 1) |V |=5, |E |=10;

Когда из любой вершины доступна любая другая вершина, то такой граф называется неориентированным связным графом (рис. 3.1). Если же граф связный, но это условие не выполняется, тогда такой граф называется ориентированным или орграфом (рис. 3.2). Ребра орграфа принято называть дугами .

В ориентированных и неориентированных графах имеется понятие степени вершины . Степень вершины – это количество ребер, соединяющих ее с другими вершинами. Степень входа вершины – количество входящих в эту вершину ребер, степень выхода – количество исходящих ребер. Сумма всех степеней графа равна удвоенному количеству всех его ребер. Для рисунка 2 сумма всех степеней равна 20.

Рисунок 3.2 – Ориентированный граф

В орграфе, в отличие от неориентированного графа, имеется возможность двигаться из вершины h в вершину s без промежуточных вершин, лишь тогда когда дуга выходит из h и входит в s , но не наоборот.

Ориентированные графы имеют следующую форму записи:

G =(V , A ), где V – вершины, A – направленные ребра.

Третий тип графов – смешанные графы (рис. 3.3). Они имеют как направленные ребра, так и ненаправленные. Формально смешанный граф записывается так: G =(V , E , A ), где каждая из букв в скобках обозначает тоже, что ей приписывалось ранее.

Рисунок 3.3 – Смешанный граф

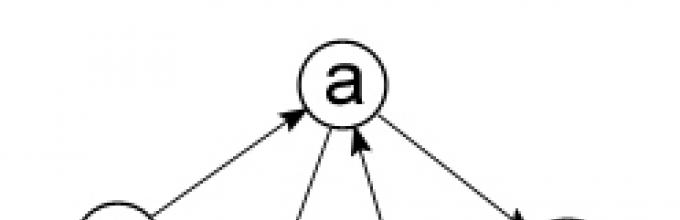
На рисунке 3 изображен смешанный граф. Одни дуги направленные [(e , a ), (e , c ), (a , b ), (c , a ), (d , b )], другие – ненаправленные [(e , d ), (e , b ), (d , c )…].

Когда у ребра оба конца совпадают, т. е. ребро выходит из некоторой вершины F и входит в нее, то такое ребро называется петлей (рис. 3.4).

Рисунок 3.4 – Петли графа

Два или более графов на первый взгляд могут показаться разными по своей структуре, что возникает вследствие различного их изображения. Но это не всегда так. Возьмем два графа (рис. 3.5). Они эквивалентны друг другу, ведь не изменяя структуру одного графа можно построить другой. Такие графы называются изоморфными , т. е. обладающими тем свойством, что какая-либо вершина с определенным числом ребер в одном графе имеет тождественную вершину в другом.

Рисунок 3.5 – Изоморфные графы

Когда каждому ребру графа поставлено в соответствие некоторое значение, называемое весом ребра , тогда такой граф взвешенный. В разных задачах в качестве веса могут выступать различные виды измерений, например длины, цены маршруты и т. п. В графическом представлении графа весовые значения указываются, как правило, рядом с ребрами.

В любом из рассмотренных нами графов имеется возможность выделить путь и, причем не один. Путь – это последовательность вершин, каждая из которых соединена с соседней вершиной посредством ребра. Если первая и последняя вершины совпадают, то такой путь называется циклом . Длина пути определяется количеством составляющих его ребер. Например, на рисунке 4.а путем служит последовательность [(e ), (a ), (b ), (c )]. Этот путь является подграфом, так как к нему применимо определение последнего, а именно: граф G’ =(V’ , E’ ) является подграфом графа G =(V , E ), только тогда когда V’ и E’ принадлежат V , E .

Граф, как и большинство других математических объектов, может быть представлен на компьютере (сохранен в его памяти). Существуют несколько способов его интерпретации, вот наиболее известные из них:

· матрица смежности;

· матрица инцидентности;

· список смежности;

· список ребер.

Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Причем размеры этих массивов, зависят от количества вершин и/или ребер в конкретном графе. Так размер матрицы смежности n ×n , где n – число вершин, а матрицы инцидентности n ×m , n – число вершин, m – число ребер в графе.

Информация о некотором реальном объекте может быть представлена по-разному. В разговорной речи мы используем словесное (вербальное) представление информации. Вот, например, словесное описание нашей области: «Волгоградская область состоит из административно-территориальных единиц - 33 районов и 6 городов областного значения. Города: Волгоград , Волжский , Камышин , Фролово , Михайловка , Урюпинск . По такому описанию можно представить как проехать из одного города в другой? (Вывод делают учащиеся.) Гораздо понятнее становится из следующей схемы (слайд 2) , по которой, например, можно ответить на вопрос: через какие города надо проехать, чтобы добраться из Волгограда в Урюпинск.

Сформулировано понятие «граф» и сети. Выделены его составные части: вершины и ребра. (Слайд 3)

Граф - это набор узлов (вершин) и связей между ними (ребер).

Сеть – граф, в котором вершины связаны между собой по принципу «многие ко многим»

Как представить информацию о графе в памяти компьютера? Хранить ее в виде рисунка (растрового или векторного) неэффективно, потому что рисунок предназначен для восприятия человеком, а не компьютером. Компьютеру удобнее всего хранить информацию в виде таблиц (массив тоже можно считать простейшей таблицей). Для описания графа часто используют квадратную таблицу, которая описывает все возможные связи между узлами (без учета дублирования). Если, например, на пересечении строки A и столбца B записано число 1, это означает, что есть ребро, соединяющее вершины A и B ; число 0 в этой ячейке означает, что такого ребра нет. Такую таблицу называют матрицей смежности. На рисунке показаны схема дорог, соответствующий ей граф и его матрица смежности: (слайд 4)

Единица на главной диагонали (выделенной серым цветом) показывает, что в графе есть петля -ребро, которое начинается и заканчивается в одной и той же вершине.
Обратите внимание, что матрица смежности симметрична относительно главной диагонали, то есть если существует ребро из вершины A в вершину B , то существует и ребро из B в A . Такой граф называют неориентированным - ребра не имеют направления и каждое из них учтено в матрице смежности дважды. Матрица смежности не дает никакой информации о том, как именно расположены узлы друг относительно друга. Для таблицы, приведенной выше, возможны, например, такие варианты, как на рисунках. (слайд 5)

Если для каждого ребра указано направление, граф называют ориентированным (или орграфом). Ребра орграфа называют дугами. Его матрица смежности не всегда симметричная. Единица, стоящая на пересечении строки A и столбца B, говорит о том, что существует дуга из вершины A в вершину B: (слайд 6).

Часто с каждым ребром связывают некоторое число - вес ребра. Это может быть, например, расстояние между городами или стоимость проезда. Такой граф называется взвешенным. Информация о таком графе хранится в виде весовой матрицы, содержащей веса ребер: (слайд 7).

У взвешенного орграфа весовая матрица не всегда симметрична относительно главной диагонали: (слайд 8).

Если связи между двумя узлами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в нее условный код, например, 0, –1 или очень большое число (?), в зависимости от задачи.

Другим примером ориентированного графа являются блок-схемы алгоритмов. (слайд 9) Блок-схема алгоритма представляет собой граф процесса управления некоторым исполнителем. Блоки – вершины этого графа – обозначают отдельные команды, которые отдаются исполнителю, а дуги указывают на последовательность переходов от одной команды к другой.

Рис. 7.1

II. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ

§ 7. Основные определения и типы графов

1. Основны е понятия

Пусть V – конечное непустое множество и Е {{u , v } u ,v V , u ≠ v } – множество его двухэлементных подмножеств. Пара G = (V, E ) называется графом . Множество V = V (G ) при этом называется множеством вершин графа G, а его элементы – вершинами; множество Е = Е (G ) называется множеством ребер графа G , а его элементы – ребрами. И вершины, и ребра графа G называются его элементами. Поэтому если u – вершина графа G , а е – ребро G , то вместо u V (G ), e E (G ) можно писать u G , e G .

Если e = {u , v } – ребро графа G (пишут также е = uv ), то вершины u и v называются концами ребра е .

Графы удобно изображать в виде рисунков, на которых вершинам соответствуют отмеченные точки (или кружочки), а ребрам – непрерывные линии, соединяющие соответствующие вершины (см. рис. 7.1).

Вершины u и v графа G называется смежными , если {u , v } E (G ), т.е. если они соединены ребром. Два ребра, в свою очередь, называются смежными , если они имеют общий конец. Если вершина v является концом ребра e , то v

и e называются инцидентными .

Мощность V (G ) множества вершин V (G ) называется порядком графа G и обозначается G . Если V (G ) = n и E (G ) =m , то граф G называется (n,m ) -графом .

2. Основные типы графов

Граф называется пустым , если E (G) = , т.е., если в нем нет ребер. Пустой граф порядка n обозначается 0 n . Граф 0 1 называется тривиальным . Граф, в котором любые две вершины соединены ребром, называется полным . Полный граф порядка n обозначается K n (рис. 7.2 – 7.5).

Граф такого вида, как на рис. 7.6, называется простой цепью . Простая цепь порядка n обозначается P n (на рис. 7.6 изображена цепь P 4 ). Простая цепь P n имеет n – 1 ребер.

Рис. 7.9

Замкнутые цепи, т.е. такие графы как на рис. 7.7, называются простыми циклами . Простой цикл порядка n обозначается C n (на рис. 7.7 изображена простая цепь С 7 ). Понятно, что простая цепь C n имеет столько же ребер, сколько и вершин, т.е. n .

Графы, такие как на рис. 7.8, называются колесами. Колесо порядка n +1 обозначается W n (на рис. 7.8 изображено колесо W 7 ); оно имеет 2n ребер.

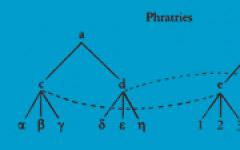
Граф называется двудольным , если множество его вершин можно разбить на два непустых подмножества (доли) так, что никакие две вершины одной доли не являются смежными. (Аналогично определяются трехдольные, четырехдольные и т.д. графы.) Таким образом, в двудольном графе смежными могут быть только вершины из разных долей (не обязательно каждая с каждой). Пример двудольного графа см. на рис. 7.9.

Если же в двудольном графе любые две вершины из разных долей соединены ребром, то такой граф называется полным двудольным .

Полный двудольный граф с n вершинами в одной доле и с m вершинами – в другой обозначается K n,m . См. примеры, приведенные на рис. 7.10 – 7.12.

	K 2,2		K 2,3		K 3,3

Графы K 1, n называется звездными графами, или звездами.

Легко видеть, что граф K n,m является (n+m, nm )- графом, т.е. имеет n+m вершин и nm ребер.

Понятно, что существуют графы, которые можно одновременно отнести к нескольким типам. Например, K 3 = C 3 , K 2 = P 2 , K 2, 2 = C 4 , K 4 = W 3 .

3. Обобщения понятия графа

Определение графа в п.1 предполагает, что любая пара вершин может быть соединена не более, чем одним ребром. Однако, существуют задачи и примеры графов,

Рис. 7.16

когда необходимо допускать существование нескольких ребер между одной и той же парой вершин. Такие ребра называются кратными . Граф с кратными ребрами называется мультиграфом (рис. 7.14). Графы, соответствующие исходному определению (в тех случаях, когда нужно подчеркнуть, что в них отсутствуют кратные ребра), называются простыми графами (рис. 7.13). Кроме того, порой приходится рассматривать ребра вида {v, v }, соединяющие вершину v саму с собой. Такие ребра называются петлями . Мультиграф с петлями называется псевдографом (рис. 7.15.).

Пара (V , E ), где V – непустое множество, а E V 2 , называется ориентированным графом (или кратко: орграфом ). Ребра такого графа представляют собой ориентированные (т.е. упорядоченные) пары вида

(u , v ). При этом, вершина u называется началом ребра , а v – концом . Ориентированные ребра называются дугами и изображаются в виде линий со стрелками, указывающими направление от начала ребра к концу

Дуги (u , v ) и (v , u ), соединяющие одну и ту же пару вершин, но имеющие противоположные направления, называются симметричными .

Можно рассматривать не только простые орграфы, но также ориентированные мульти- и псевдографы.

Иногда при решении некоторых задач ребрам и (или) вершинам ставят в соответствие некоторые числа. Независимо от их конкретного смысла, такие числа называют весами (вес вершины, вес ребра), а полученный граф называется взвешенным графом .

Как правило, при изучении тех или иных вопросов, заранее оговаривается (или ясно из контекста) о каких графах идет речь. В этом случае их просто называют графами без приставок "мульти-", "псевдо-" и т.д.

4. Изоморфные графы

Одной из особенностей графов является то, что при их изображении на плоскости совершенно не важно, как расположены вершины друг относительно друга. Поэтому одному и тому графу могут соответствовать различные его изображения. Кроме того, именно такие рисунки, представляющие собой простейший способ задания

графа, зачастую и называют графами. Чтобы отличать рисунки, отвечающие одному и тому же графу, от рисунков, изображающих различные графы, введем следующее понятие.

Определение . Два графа G и H называются изоморфными , если существует биекция f : V (G ) → V (H ), сохраняющая смежность, т.е. такое биективное отображение, при котором образы вершин v и u графа G смежны в H тогда и только тогда, когда u и v смежны в графе G . Отображение f , обладающее указанным свойством, называется

изоморфизмом.

Если графы G и H изоморфны, то пишут G H .

Например, все три графа на рис. 7.17-7.19 изоморфны друг другу (изоморфизм определяется нумерацией вершин).

Очевидно, что отношение изоморфности на множестве графов является отношением эквивалентности (оно рефлексивно, симметрично и транзитивно). Следовательно, множество всех графов разбивается на классы изоморфных графов так, что разные классы не пересекаются. Все графы, попадающие в один класс естественно отождествлять, т.е. считать совпадающими (они могут отличаться лишь рисунком или природой своих элементов). В тех случаях, когда нужно подчеркнуть, что рассматриваемые графы отличаются лишь с точностью до изоморфизма, принято говорить об "абстрактных графах ". По сути дела, абстрактный граф – это класс изоморфных графов.

В некоторых ситуациях все же приходится различать изоморфные графы и тогда возникает понятие "помеченный граф ". Граф порядка n называется помеченным, если его вершинам присвоены метки, например, номера 1, 2, 3, …, n . В этом случае вершины графа G отождествляют с их номерами, т.е. полагают, что V (G ) = {1, 2, 3, …, n }.

Вполне несвязные графы . Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Будем обозначать вполне несвязный граф с п вершинами через N n ; N 4 показан на рис. 1. Заметим, что у вполне несвязного графа все вершины изолированы. Вполне несвязные графы не представляют особого интереса.

Полные графы . Простой граф, в котором любые две вершины смежны, называется полным графом. Полный граф с n вершинами обычно обозначается через. Графы и изображены на рис. 2 и 3. имеет ровно n (n - 1)/2 ребер.

Регулярные графы . Граф, у которого все вершины имеют одну и ту же степень, называется регулярным графом. Если степень каждой вершины равна r, то граф называется регулярным степени r. Регулярные графы степени 3, называемые также кубическими (или трехвалентными) графами (см., например, рис. 2 и 4). Другим известным примером кубического графа является так называемый граф Петерсена, показанный на рис. 5. Отметим, что каждый вполне несвязный граф является регулярным степени 0, а каждый полный граф К n - регулярным степени n - 1.

Платоновы графы . Среди регулярных графов особенно интересны так называемые Платоновы графы - графы образованные вершинами и ребрами пяти правильных многогранников - платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра. Граф соответствует тетраэдру (рис. 2); графы, соответствующие кубу и октаэдру, показаны на рис. 5 и 6;

Двудольные графы . Допустим, что множество вершин графа можно разбить на два непересекающихся подмножества V 1 и V 2 так, что каждое ребро в G соединяет какую-нибудь вершину из V 1 с какой-либо вершиной из V 2 (рис. 7);

тогда G называется двудольным графом. Такие графы иногда обозначают G(V 1, V 2), если хотят выделить два указанных подмножества. Двудольный граф можно определить и по-другому - в терминах раскраски его вершин двумя цветами, скажем красным и синим. При этом граф называется двудольным, если каждую его вершину можно окрасить красным или синим цветом так, чтобы любое ребро имело один конец красный, а другой - синий. Следует подчеркнуть, что в двудольном графе совсем не обязательно каждая вершина из V 1 соединена с каждой вершиной из V 2 ; если же это так и если при этом граф G простой, то он называется полным двудольным графом и обычно обозначается где m, n - число вершин соответственно в V 1 и V 2 . Например, на рис. 8 изображен граф K 4 , 3 . Заметим, что граф имеет ровно m + n вершин и mn ребер. Полный двудольный граф вида называется звездным графом; на рис. 9 изображен звездный граф.

Связные графы . Граф связный, если его нельзя представить в виде объединения двух графов, и несвязный в противном случае. Очевидно, что всякий несвязный граф G можно представить в виде объединения конечного числа связных графов - каждый из таких связных графов называется компонентой (связности) графа G. (На рис. 10 изображен граф с тремя компонентами.) Доказательство некоторых утверждений для произвольных графов часто бывает удобно сначала провести для связных графов, а затем применить их к каждой компоненте в отдельности.

Перед тем как начать изучение непосредственно алгоритмов, необходимо обладать базовыми знаниями касательно самих графов, понимать, как они представляются в компьютере. Здесь не будут подробно описаны все аспекты теории графов (этого и не требуется), но только те, незнание которых заметно усложнит усвоение данной области программирования.

Несколько примеров дадут немного поверхностного представления о графе. Так типичным графом является схема метро или какой-либо другой маршрут. В частности программисту знакома компьютерная сеть, также являющаяся графом. Общее здесь это наличие точек, соединенных линиями. Так в компьютерной сети точки – это отдельные серверы, а линии – различные виды электрических сигналов. В метрополитене первое – станции, второе – туннели, проложенные между ними. В теории графов точки именуется вершинами (узлами ), а линии – ребрами (дугами ). Таким образом, граф – это совокупность вершин, соединённых ребрами.

Математика оперирует не содержанием вещей, а их структурой, абстрагируя ее из всего того, что дано как целое. Пользуясь именно этим приемом, мы можем заключать о каких-либо объектах как о графах. А поскольку теория графов это часть математики, то для нее нет абсолютно никакого значения, что в принципе представляет собой объект; важно лишь то, является ли он графом, т. е. обладает ли обязательными для графов свойствами. Поэтому, прежде чем привести примеры, мы выделяем в рассматриваемом объекте лишь то, что как нам кажется, позволит показать аналогию, отыскиваем общее.

Вернемся к компьютерной сети. Она обладает определенной топологией, и может быть условно изображена в виде некоторого числа компьютеров и путей их соединяющих. На рисунке ниже в качестве примера показана полносвязная топология.

Это по сути граф. Пять компьютеров являются вершинами, а соединения (пути передачи сигналов) между ними – ребрами. Заменив компьютеры вершинами, мы получим математический объект – граф, который имеет 10 ребер и 5 вершин. Пронумеровать вершины можно произвольным образом, а не обязательно так, как это сделано на рисунке. Стоит отметить, что в данном примере не используется ни одной петли, то есть такого ребра, которое выходит из вершины и сразу же входит в нее, но петли могут встречаться в задачах.

Вот некоторые важные обозначения, используемые в теории графов:

• G=(V, E), здесь G – граф, V – его вершины, а E – ребра;
• |V| – порядок (число вершин);
• |E| – размер графа (число рёбер).

В нашем случае (рис. 1) |V|=5, |E|=10;

Когда из любой вершины доступна любая другая вершина, то такой граф называется неориентированным связным графом (рис. 1). Если же граф связный, но это условие не выполняется, тогда такой граф называется ориентированным или орграфом (рис. 2).

В ориентированных и неориентированных графах имеется понятие степени вершины. Степень вершины – это количество ребер, соединяющих ее с другими вершинами. Сумма всех степеней графа равна удвоенному количеству всех его ребер. Для рисунка 2 сумма всех степеней равна 20.

В орграфе, в отличие от неориентированного графа, имеется возможность двигаться из вершины h в вершину s без промежуточных вершин, лишь тогда когда ребро выходит из h и входит в s, но не наоборот.

Ориентированные графы имеют следующую форму записи:

G=(V, A), где V – вершины, A – направленные ребра.

Третий тип графов – смешанные графы (рис. 3). Они имеют как направленные ребра, так и ненаправленные. Формально смешанный граф записывается так: G=(V, E, A), где каждая из букв в скобках обозначает тоже, что ей приписывалось ранее.

В графе на рисунке 3 одни дуги направленные [(e, a), (e, c), (a, b), (c, a), (d, b)], другие – ненаправленные [(e, d), (e, b), (d, c)…].

Два или более графов на первый взгляд могут показаться разными по своей структуре, что возникает вследствие различного их изображения. Но это не всегда так. Возьмем два графа (рис. 4).

Они эквивалентны друг другу, ведь не изменяя структуру одного графа можно построить другой. Такие графы называются изоморфными , т. е. обладающими тем свойством, что какая-либо вершина с определенным числом ребер в одном графе имеет тождественную вершину в другом. На рисунке 4 изображены два изоморфных графа.

Когда каждому ребру графа поставлено в соответствие некоторое значение, называемое весом ребра, тогда такой граф взвешенный . В разных задачах в качестве веса могут выступать различные виды измерений, например длины, цены маршруты и т. п. В графическом представлении графа весовые значения указываются, как правило, рядом с ребрами.

В любом из рассмотренных нами графов имеется возможность выделить путь и, причем не один. Путь – это последовательность вершин, каждая из которых соединена с последующей посредством ребра. Если первая и последняя вершины совпадают, то такой путь называется циклом. Длина пути определяется количеством составляющих его ребер. Например, на рисунке 4.а путем служит последовательность [(e), (a), (b), (c)]. Этот путь является подграфом, так как к нему применимо определение последнего, а именно: граф G’=(V’, E’) является подграфом графа G=(V, E), только тогда когда V’ и E’ принадлежат V, E.