Сколько асимптот может быть у графика функции?

Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции. Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса - бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.

Что значит найти асимптоты графика функции?

Это значит выяснить их уравнения, ну и начертить прямые линии, если того требует условие задачи. Процесс предполагает нахождение пределов функции.

Вертикальные асимптоты графика функции

Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.

Примечание: обратите внимание, что запись используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой - зависит от контекста.

Таким образом, чтобы установить наличие вертикальной асимптоты в точке достаточно показать, что хотя бы один из односторонних пределов бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова - любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: и ось ординат.

Из вышесказанного также следует очевидный факт: если функция непрерывна на, то вертикальные асимптоты отсутствуют. На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)

Обратное утверждение в общем случае неверно: так, функция не определена на всей числовой прямой, однако совершенно обделена асимптотами.

Наклонные асимптоты графика функции

Наклонные (как частный случай - горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше 2-х наклонных асимптот. Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при, а график арктангенса при - двумя такими асимптотами, причём различными.

Асимптоты графика функции

Асимптотой графика функции y = f(x) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

На рисунке 3.10. приведены графические примеры вертикальной , горизонтальных и наклонной асимптот.

Нахождение асимптот графика основано на следующих трех теоремах.

Теорема о вертикальной асимптоте. Пусть функция у = f(х) определена в некоторой окрестности точки x 0 (исключая, возможно, саму эту точку) и хотя бы один из односторонних пределов функции равен бесконечности, т.е. Тогда прямая x = x 0 является вертикальной асимптотой графика функции у = f(х).

Очевидно, что прямая х = х 0 не может быть вертикальной асимптотой, если функция непрерывна в точке х 0 , так как в этом случае . Следовательно, вертикальные асимптоты следует искать в точках разрыва функции или на концах ее области определения.

Теорема о горизонтальной асимптоте. Пусть функция у = f(х) определена при достаточно больших х и существует конечный предел функции . Тогда прямая у = b есть горизонтальная асимптота графика функции.

Замечание. Если конечен только один из пределов , то функция имеет соответственно левостороннюю либо правостороннюю горизонтальную асимптоту.

В том случае, если , функция может иметь наклонную асимптоту.

Теорема о наклонной асимптоте. Пусть функция у = f(х) определена при достаточно больших х и существуют конечные пределы . Тогда прямая y = kx + b является наклонной асимптотой графика функции.

Без доказательства.

Наклонная асимптота, так же, как и горизонтальная, может быть правосторонней или левосторонней, если в базе соответствующих пределов стоит бесконечность определенного знака.

Исследование функций и построение их графиков обычно включает следующие этапы:

1. Найти область определения функции.

2. Исследовать функцию на четность-нечетность.

3. Найти вертикальные асимптоты, исследовав точки разрыва и поведение функции на границах области определения, если они конечны.

4. Найти горизонтальные или наклонные асимптоты, исследовав поведение функции в бесконечности.

Гиперболой называется геометрическое место точек, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (эта постоянная должна быть положительной и меньше расстояния между фокусами).

Обозначим эту постоянную через 2а, расстояние между фокусами через и выберем оси координат так же, как и в § 3. Пусть - произвольная точка гиперболы.

По определению гиперболы

В правой части равенства нужно выбрать знак плюс, если и знак минус, если

Так как то последнее равенство можно записать в виде:

Это и есть уравнение гиперболы в выбранной системе координат.

Освобождаясь в этом уравнении от радикалов (как и в § 3), можно привести уравнение к простейшему виду.

Перенося первый радикал в правую часть равенства и возводя обе части в квадрат, после очевидных преобразований получим:

Возведя еще раз обе части равенства в квадрат, сделав приведение подобных членов и разделив на свободный член, получим:

Так как , то величина положительна. Обозначая ее через , т. е. полагая

получим каноническое уравнение гиперболы.

Исследуем форму гиперболы.

1) Симметрии гиперболы. Так как уравнение (3) содержит только квадраты текущих координат, то оси координат являются осями симметрии гиперболы (см. аналогичное утверждение для эллипса). Ось симметрии гиперболы, на которой располагаются фокусы, называется фокальной осью. Точка пересечения осей симметрии - центр симметрии - называется центром гиперболы. Для гиперболы, заданной уравнением (3), фокальная ось совпадает с осью Ох, а центром является начало координат.

2) Точки пересечения с осями симметрии. Найдем точки пересечения гиперболы с осями симметрии - вершины гиперболы. Полагая в ураннении найдем абсциссы точек пересечения гиперболы с осью

Следовательно, точки являются вершинами гиперболы (рис. 51); расстояние между ними равно 2а. Чтобы найти точки пересечения с осью Оу, положим в уравнении Получим для определения ординат этих точек уравнение

т. е. для у мы получили мнимые значения; это означает, что ось Оу не пересекает гиперболы.

В соответствии с этим ось симметрии, пересекающая гиперболу, называется действительной осью симметрии (фокальной осью), ось симметрии, которая не пересекает гиперболы, называется мнимой осью симметрии. Для гиперболы, заданной уравнением (3), действительной осью симметрии является ось , мнимой осью симметрии - ось Отрезок соединяющий вершины гиперболы, а также его длина 2а называются действительной осью гиперболы. Если на мнимой оси симметрии гиперболы отложить в обе стороны от ее центра О отрезки ОБ, и длиною b, то отрезок а также его длина называются мнимой осью гиперболы. Величины а и b называются соответственно действительной и мнимой полуосями гиперболы.

3) Форма гиперболы. При исследовании формы гиперболы достаточно рассматривать положительные значения х и у, потому что кривая симметрично расположена относительно осей координат.

Так как из уравнения (3) следует, что 1, то может изменяться от а до Когда увеличивается от а до то У тоже увеличивается от 0 до Кривая имеет форму, изображенную на рис. 51. Она располагается вне полосы, ограниченной прямыми и состоит из двух отдельных ветвей. Для любой точки М одной из этих ветвей (правая ветвь), для любой точки М другой ветви (левая ветвь).

4) Асимптоты гиперболы. Чтобы более ясно представить себе вид гиперболы, рассмотрим две прямые линии, тесно с нею связанные - так называемые асимптоты.

Предполагая х и у положительными, разрешим уравнение (3) гиперболы относительно ординаты у:

Сопоставим уравнение с уравнением прямой линии называя соответствующими две точки расположенные соответственно на этой прямой и на гиперболе и имеющие одну и ту же абсциссу (рис. 51). Очевидно, и разность Y - у ординат соответствующих точек выражает расстояние между ними, т. е.

Покажем, что при неограниченном возрастании расстояние MN, убивая, стремится к нулю. В самом деле,

После упрощения получим:

Из последней формулы мы усматриваем, что при неограниченном возрастании абсциссы расстояние MN убывает и стремится к нулю. Отсюда следует, что когда точка М, двигаясь по гиперболе в первом квадранте, удаляется в бесконечность, то ее расстояние до прямой уменьшается и стремится к нулю. То же обстоятельство будет иметь место при движении точки М по гиперболе в третьем квадранте (вследствие симметрии относительно начала координат О).

Наконец, вследствие симметрии гиперболы относительно оси Оу мы получим вторую прямую симметрично расположенную с прямой к которой также будет неограниченно приближаться точка М при движении по гиперболе и удалении в бесконечность (во втором и четвертом квадрантах).

Эти две прямые линии носят название асимптот гиперболы, они, как мы видели, имеют уравнения:

Очевидно, асимптоты гиперболы располагаются по диагоналям прямоугольника, одна сторона которого параллельна оси Ох и равна 2а, другая - параллельна оси Оу и равна а центр лежит в начале координат (см. рис. 51).

При вычерчивании гиперболы по ее уравнению рекомендуется предварительно построить ее асимптоты.

Равносторонняя гипербола. В случае гипербола называется равносторонней; ее уравнение получается из (3) и имеет вид:

Очевидно, угловые коэффициенты асимптот для равносторонней гиперболы будут Следовательно, асимптоты равносторонней гиперболы перпендикулярны между собой и делят пополам углы между ее осями симметрии.

Во многих случаях построение графика функции облегчается, если предварительно построить асимптоты кривой.

Определение 1. Асимптотами называются такие прямые , к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.

Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

Вертикальные асимптоты

Определение . Прямая x = a является вертикальной асимптотой графика функции , если точка x = a является точкой разрыва второго рода для этой функции.

Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f (x ) , если выполняется хотя бы одно из условий:

При этом функция f (x ) может быть вообще не определена соответственно при x ≥ a и x ≤ a .

Замечание:

Пример 1. График функции y =lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy ) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:

(рис. сверху).

самостоятельно, а затем посмотреть решения

Пример 2. Найти асимптоты графика функции .

Пример 3. Найти асимптоты графика функции

Горизонтальные асимптоты

Если (предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b ), то y = b – горизонтальная асимптота кривой y = f (x ) (правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности, и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).

Пример 5. График функции

при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox ), так как предел функции при стремлении "икса" к минус бесконечности равен нулю:

Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении "икса" к плюс бесконечности равен бесконечности:

Наклонные асимптоты

Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны осям координат, поэтому для их построения нам требовалось лишь определённое число - точка на оси абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше - угловой коэффициент k , который показывает угол наклона прямой, и свободный член b , который показывает, насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию, а из неё - уравнения прямой, заметят, что для наклонной асимптоты находят уравнение прямой с угловым коэффициентом . Существование наклонной асимптоты определяется следующей теоремой, на основании которой и находят названные только что коэффициенты.

Теорема. Для того, чтобы кривая y = f (x ) имела асимптоту y = kx + b , необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:

(1)

(2)

Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.

В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.

При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.

При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.

Если хотя бы один из пределов, определяющих асимптоту y = kx + b , не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).

Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0 .

Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.

Пример 6. Найти асимптоты графика функции

Решение. Функция определена на всей числовой прямой, кроме x = 0 , т.е.

Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:

Следовательно, x = 0 – вертикальная асимптота графика данной функции.

Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:

Выясним наличие наклонной асимптоты:

Получили конечные пределы k = 2 и b = 0 . Прямая y = 2x является двусторонней наклонной асимптотой графика данной функции (рис. внутри примера).

Пример 7. Найти асимптоты графика функции

Решение. Функция имеет одну точку разрыва x = −1 . Вычислим односторонние пределы и определим вид разрыва:

Заключение: x = −1 - точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.

Ищем наклонные асимптоты. Так как данная функция - дробно-рациональная, пределы при и при будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой - наклонной асимптоты:

Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:

y = −3x + 5 .

На рисунке график функции обозначен бордовым цветом, а асимптоты - чёрным.

Пример 8. Найти асимптоты графика функции

Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:

Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .

Пример 9. Найти асимптоты графика функции

Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения функции. Функция определена, когда выполняется неравенство и при этом . Знак переменной x совпадает со знаком . Поэтому рассмотрим эквивалентное неравенство . Из этого получаем область определения функции: . Вертикальная асимптота может быть только на границе области определения функции. Но x = 0 не может быть вертикальной асимптотой, так как функция определена при x = 0 .

Рассмотрим правосторонний предел при (левосторонний предел не существует):

Точка x = 2 - точка разрыва второго рода, поэтому прямая x = 2 - вертикальная асимптота графика данной функции.

Ищем наклонные асимптоты:

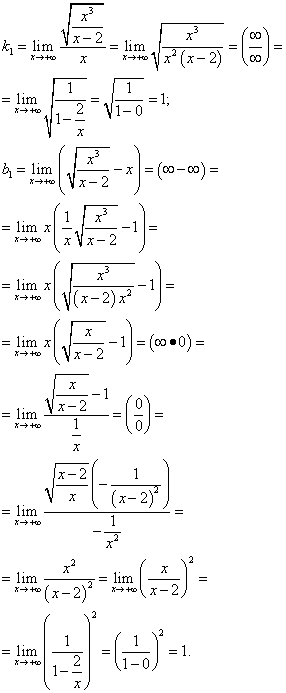
Итак, y = x + 1 - наклонная асимптота графика данной функции при . Ищем наклонную асимптоту при :

Итак, y = −x − 1 - наклонная асимптота при .

Пример 10. Найти асимптоты графика функции

Решение. Функция имеет область определения . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при .

Асимптоты графика функции

Призрак асимптоты давно бродил по сайту чтобы, наконец, материализоваться в отдельно взятой статье и привести в особый восторг читателей, озадаченных полным исследованием функции . Нахождение асимптот графика – одна из немногих частей указанного задания, которая освещается в школьном курсе лишь в обзорном порядке, поскольку события вращаются вокруг вычисления пределов функций , а они относятся всё-таки к высшей математике. Посетители, слабо разбирающиеся в математическом анализе, намёк, думаю, понятен;-) …стоп-стоп, вы куда? Пределы – это легко!

Примеры асимптот встретились сразу же на первом уроке о графиках элементарных функций , и сейчас тема получает детальное рассмотрение.

Итак, что такое асимптота?

Представьте переменную точку , которая «ездит» по графику функции. Асимптота – это прямая , к которой неограниченно близко приближается график функции при удалении его переменной точки в бесконечность.

Примечание : определение содержательно, если вам необходима формулировка в обозначениях математического анализа, пожалуйста, обратитесь к учебнику.

На плоскости асимптоты классифицируют по их естественному расположению:

1) Вертикальные асимптоты , которые задаются уравнением вида , где «альфа» – действительное число. Популярная представительница определяет саму ось ординат,
с приступом лёгкой тошноты вспоминаем гиперболу .

2) Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом . Иногда отдельной группой выделяют частный случай – горизонтальные асимптоты . Например, та же гипербола с асимптотой .

Резво пошло-поехало, ударим по теме короткой автоматной очередью:

Сколько асимптот может быть у графика функции?

Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции . Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса – бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.

Что значит ?

Вертикальные асимптоты графика функции

Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.

Примечание : обратите внимание, что запись используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой – зависит от контекста.

Таким образом, чтобы установить наличие вертикальной асимптоты в точке достаточно показать, что хотя бы один из односторонних пределов бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции . Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова – любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: и ось ординат (см. Графики и свойства элементарных функций ).

Из вышесказанного также следует очевидный факт: если функция непрерывна на , то вертикальные асимптоты отсутствуют . На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)

Наклонные асимптоты графика функции

Наклонные (как частный случай – горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше двух наклонных асимптот . Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при , а график арктангенса при – двумя такими асимптотами, причём различными.

Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью . Например, …правильно догадались: .

Общее практическое правило :

Если существуют два конечных предела , то прямая является наклонной асимптотой графика функции при . Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.

Примечание : формулы остаются справедливыми, если «икс» стремится только к «плюс бесконечности» или только к «минус бесконечности».

Покажем, что у параболы нет наклонных асимптот:

Предел бесконечен, значит, наклонная асимптота отсутствует. Заметьте, что в нахождении предела необходимость отпала, поскольку ответ уже получен.

Примечание : если у вас возникли (или возникнут) трудности с пониманием знаков «плюс-минус», «минус-плюс», пожалуйста, посмотрите справку в начале урока
о бесконечно малых функциях , где я рассказал, как правильно интерпретировать данные знаки.

Очевидно, что у любой квадратичной, кубической функции, многочлена 4-й и высших степеней также нет наклонных асимптот.

А теперь убедимся, что при у графика тоже нет наклонной асимптоты. Для раскрытия неопределённости используем правило Лопиталя :
, что и требовалось проверить.

При функция неограниченно растёт, однако не существует такой прямой, к которой бы её график приближался бесконечно близко .

Переходим к практической части урока:

Как найти асимптоты графика функции?

Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса – речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться). Начнём с чего-нибудь простого:

Пример 1

Найти асимптоты графика функции

Решение удобно разбить на два пункта:

1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при , и сразу понятно, что в данной точке функция терпит бесконечный разрыв , а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:

Напоминаю технику вычислений, на которой я подобно останавливался в статье Непрерывность функции. Точки разрыва . В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
.

А вот в знаменателе получается бесконечно малое отрицательное число :
, оно и определяет судьбу предела.

Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого – они ПОМОГАЮТ ПОНЯТЬ, КАК расположен график функции и построить его КОРРЕКТНО . Поэтому обязательно вычислим и правосторонний предел:

Вывод : односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при .

Первый предел конечен , значит, необходимо «продолжить разговор» и найти второй предел:

Второй предел тоже конечен .

Таким образом, наша асимптота:

Вывод : прямая, заданная уравнением является горизонтальной асимптотой графика функции при .

Для нахождения горизонтальной асимптоты
можно пользоваться упрощенной формулой :

Если существует конечный предел , то прямая является горизонтальной асимптотой графика функции при .

Нетрудно заметить, что числитель и знаменатель функции одного порядка роста , а значит, искомый предел будет конечным:

Ответ :

По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции , то на черновике сразу же делаем набросок:

Исходя из трёх найденных пределов , попытайтесь самостоятельно прикинуть, как может располагаться график функции . Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции , и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.

Пример 2

Найти асимптоты графика функции

Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта – вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдена по упрощенной схеме.

На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:

Пример 3

Найти асимптоты графика функции

Решение : Раз, два и готово:

1) Вертикальные асимптоты находятся в точках бесконечного разрыва , поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение :

Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется =)

В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители :
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.

Перепишем функцию в виде

Найдём односторонние пределы в точке :

И в точке :

Таким образом, прямые являются вертикальными асимптотами графика рассматриваемой функции.

2) Если посмотреть на функцию , то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:

Таким образом, прямая (ось абсцисс) является горизонтальной асимптотой графика данной функции.

Ответ :

Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:

Схематично изобразите вашу версию графика на черновике.

Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции . Правильная картинка – в конце урока.

Пример 4

Найти асимптоты графика функции

Пример 5

Найти асимптоты графика функции

Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4 порядок роста знаменателя больше , чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста . В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая – через предел .

Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:

Пример 6

Найти асимптоты графика функции

Решение : классика жанра:

1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово – отлично! Пункт №1 закрыт.

2) Проверим наличие наклонных асимптот:

Первый предел конечен , поэтому едем дальше. В ходе вычисления второго предела для устранения неопределённости «бесконечность минус бесконечность» приводим выражение к общему знаменателю:

Второй предел тоже конечен , следовательно, у графика рассматриваемой функции существует наклонная асимптота:

Вывод :

Таким образом, при график функции бесконечно близко приближается к прямой :

Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы – важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).

Пример 7

Найти асимптоты графика функции

Решение : комментировать особо нечего, поэтому оформлю примерный образец чистового решения:

1) Вертикальные асимптоты. Исследуем точку .

Прямая является вертикальной асимптотой для графика при .

2) Наклонные асимптоты:

Прямая является наклонной асимптотой для графика при .

Ответ :

Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.

Пример 8

Найти асимптоты графика функции

Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.

Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше – наклонной асимптоты уже не будет (например, ).

Но в жизни происходят и другие чудеса:

Пример 9

Пример 11

Исследовать график функции на наличие асимптот

Решение : очевидно, что , поэтому рассматриваем только правую полуплоскость, где есть график функции.

Таким образом, прямая (ось ординат) является вертикальной асимптотой для графика функции при .

2) Исследование на наклонную асимптоту можно провести по полной схеме, но в статье Правила Лопиталя мы выяснили, что линейная функция более высокого порядка роста, чем логарифмическая, следовательно: (см. Пример 1 того же урока).